SVM支持向量机的理解与推导 - liuyangfei的博客

第一部分：样本集线性可分

给定训练样本集$D={(x_1,y_1),(x_2,y_2),…,(x_n,y_N)}$，其中$y_i\in{(-1, 1)}$分类学习的目的是在样本空间中找到一个划分超平面，将不同类划分开。但是能将训练样本划分开的超平面有很多，SVM的选择方式就是最大化两个异类样本之间的间隔。下图来自知乎-支持向量机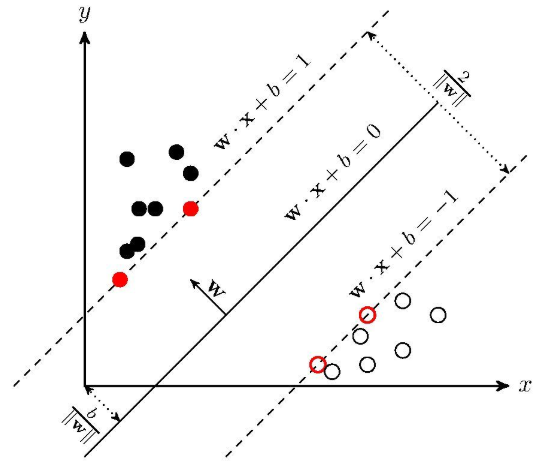

在线性空间中，划分超平面可以用如下的线性方程表示： $w^Tx+b=0 \tag{1} \label{eq1}$ 因此，对于$y=1$这一类有$w^Tx+b\geq 0$，而$y=-1$这一类有$w^Tx+b\leq 0$。我们总可以通过缩放变换使得下式成立： $w^Tx+b\geq +1,\qquad y_i=+1;\\ w^Tx+b\leq -1,\qquad y_i=-1;\tag{2} \label{eq2}$ 我们定义样本的函数间隔为 $\hat r = y_i(w^Tx_i+b)\tag{3}\label{eq3}$ 样本的函数间隔可以反应两个异类样本之间的间距，$\hat r$ 越大，则间距越大。但是SVM却不是直接最大化函数间隔来寻找超平面，因为如果我们等比例的放大$w,b$，那么函数间隔 $\hat r$ 会增大，但是超平面的位置却没有改变。

几何间隔 样本空间中任意 $x$ 到超平面的距离可写为 $r=\frac{|w^Tx+b|}{\|w\|}\tag{4}\label{4}$ 能够使得$\eqref{eq2}$式成立的样本称为“支持向量”，因此两个异类支持向量到超平面的距离为 $r=\frac{2}{\|w\|}\tag{5}\label{eq5}$ 因此要找到最大间隔的划分超平面，就是最大化$\eqref{eq5}$式，即 $\max_{w,b} \quad \frac{2}{\|w\|}\\ s.t. \quad y_i(w^Tx+b)\geq 1,\quad i=1,2,...n\tag{6}\label{eq6}$ PS：这里有个小疑问，得到$\eqref{eq5}$式的条件是选择两个异类支持向量，那么为什么最大化间隔时需要用到所有的样本呢？

我的理解是本来应该最大化所有样本到超平面的间隔，但是这些间隔有一个下确界，就是异类支持向量到超平面的距离，所以直接最大化这个距离就可以了，但是我们又不知道哪些样本是支持向量，因此需要用到所有的样本。

$\eqref{eq6}$式可以转化为 $\min_{w,b} \quad \frac{1}{2}\|w\|^2 \\ s.t. \quad y_i(w^Tx+b)\geq 1,\quad i=1,2,...n\tag{7}\label{eq7}$ 如何求解$\eqref{eq7}$式？第一种方法可以直接使用优化计算包，该问题本身是一个凸二次规划问题；第二种方法是求解其对偶问题。

为什么转化为对偶问题？

求解更加高效
可以方便的引入核函数

使用拉格朗日乘子法转化为对偶问题，则该问题的拉格朗日函数为 $L(w,b,\alpha) =\frac{1}{2}\|w\|^2+\sum_{i=1}^n\alpha_i(1-y_i(w^Tx_i+b))\tag{8}\label{eq8}$ 因此，原问题$\eqref{eq7}$式就转化为 $\theta(w^*,b^*,\alpha^*)=\arg\min_{w,b}\arg\max_\alpha \quad L(w,b,\alpha)\tag{9}\label{eq9}$ $\eqref{eq9}$式的求解需要转化为求解对偶问题，满足KKT条件 $\alpha_i \geq 0 \\ y_i(w^Tx+b)-1\geq 0\\ \alpha_i(1-y_i(w^Tx_i+b)) = 0\tag{10}\label{eq10}$ 这里的KKT条件另有用处，后面再说。

因此，最终求解目标为 $\theta(w^*,b^*,\alpha^*)=\arg\max_\alpha\arg\min_{w,b} \quad L(w,b,\alpha)\tag{11}\label{eq11}$ $\eqref{eq11}$式先对 $w,b$ 求偏导，得到 $w=\sum_{i=1}^n\alpha_i y_i x_i\\ \sum_{i=1}^n\alpha_iy_i=0\tag{12}\label{eq12}$ 将$\eqref{eq12}$式代入$\eqref{eq8}$式 $\begin{equation} \begin{split} L(w,b,\alpha)&=\frac{1}{2}\|w\|^2+\sum_{i=1}^n\alpha_i(1-y_i(w^Tx_i+b))\\ &=\frac{1}{2}\|w\|^2+\sum_{i=1}^n\alpha_i-\sum_{i=1}^n\alpha_iy_iw^Tx_i-\sum_{i=1}^n\alpha_iy_ib\\ &=\frac{1}{2}w^T\sum_{i=1}^n\alpha_i y_i x_i+\sum_{i=1}^n\alpha_i-w^T\sum_{i=1}^n\alpha_iy_ix_i\\ &=-\frac{1}{2}w^T\sum_{i=1}^n\alpha_i y_i x_i+\sum_{i=1}^n\alpha_i\\ &=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_j y_iy_jx_i^Tx_i \end{split} \end{equation}\tag{13}\label{eq13}$ 因此，$\eqref{eq7}$式对应的对偶问题为 $\max_\alpha\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_j y_iy_jx_i^Tx_j \\ s.t.\quad\sum_{i=1}^n\alpha_iy_i=0\\ \alpha_i\geq 0\tag{14}\label{eq14}$ 求解出 $\alpha$ 就可以根据$\eqref{eq12}$式求解 $w$，如何求解 $b$ ？

假设 $x_i$ 为正类支持向量，$x_j$ 为负类支持向量，则有 ${w^*}^Tx_i+b=1\\ {w^*}^Tx_j+b=-1\\\tag{15}\label{eq15}$ 因此，有 $b^*=-\frac{\min_{y_i=1}{w^*}^Tx_i+\max_{y_j=-1}{w^*}^Tx_j}{2}\tag{16}\label{eq16}$ 关于$\eqref{eq14}$式求解 $\alpha_i$ 所用的SMO算法还不了解，了解以后有机会再补。

至此，样本空间线性可分的SVM结束，根据$\eqref{eq10}$式的KKT条件以及$\eqref{eq8}$式，我们可以得到

若 $\alpha_i =0$，则该样本不会对$\eqref{eq8}$ 式产生影响；若 $\alpha_i\neq0$，则必有 $1-y_i(w^Tx_i+b)=0$，对应的是支持向量，因此，支持向量机训练完成后，最终模型只与支持向量有关。

第二部分：样本集线性不可分

第一部分是样本空间线性可分的情况，如果样本空间线性不可分，又该如何处理？

对于这样的问题，可将样本空间映射到一个更高维的特征空间，使得在这个特征空间中线性可分。（这里所用的样本空间其实也是样本的特征所张成的一个空间，跟特征空间是一个意思）。因此在高维特征空间中划分超平面所对应的模型为 $w^T\phi(x)+b=0\tag{17}\label{eq17}$ 对应的$\eqref{eq7}$式为 $\min_{w,b} \quad \frac{1}{2}\|w\|^2 \\ s.t. \quad y_i(w^T\phi(x)+b)\geq 1,\quad i=1,2,...n\tag{18}\label{eq18}$ 其对偶问题为 $\max_\alpha\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_j y_iy_j\phi(x_i)^T\phi(x_j) \\ s.t.\quad\sum_{i=1}^n\alpha_iy_i=0\\ \alpha_i\geq 0\tag{19}\label{eq19}$ 该式中设计到高维空间的内积计算，通常非常困难，因此，设想有这样一个核函数 $k(x_i,x_j)=\phi(x_i)^T\phi(x_j)\tag{20}\label{eq20}$ 则$\eqref{eq19}$式为 $\max_\alpha\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_j y_iy_jk(x_i,x_j) \\ s.t.\quad\sum_{i=1}^n\alpha_iy_i=0\\ \alpha_i\geq 0\tag{21}\label{eq21}$ 至此，线性不可分问题已经可以解决了，但是为什么总有一个核函数能够满足$\eqref{eq20}$式呢？详细请参考西瓜书第一版P128。

常用的核函数有以下几种

线性核	$k(x_i,x_j)=x_i^Tx_j$
多项式核	$k(x_i,x_j)=(x_i^Tx_j)^d$，$d$ 是多项式次数
高斯核	$k(x_i,x_j)=\exp(-\frac{\|x_i-x_j\|^2}{2\sigma})$
拉普拉斯核	$k(x_i,x_j)=\exp(-\frac{\|x_i-x_j\|}{\sigma}$
Sigmoid核	$k(x_i,x_j)=tanh(\beta x_i^Tx_j+\theta)$

第三部分：软间隔与正则化

前面所讲的都是在不允许错分的情况下，但是现实中很难找到一个超平面，即便找到了也不确定是否过拟合，因此我们允许SVM在一些样本上出错。因此引入“软间隔”

硬间隔时样本满足的约束是 $\quad y_i(w^Txi+b)\geq 1\tag{22}\label{eq22}$ 因此，软间隔时可以允许一些样本不满足上式。但是，在最大化间隔的同时，希望不满足约束的样本越少越好，于是，优化目标为 $\min_{w,b}\quad \frac{1}{2}\|w\|^2+\lambda\sum_{i=1}^{n}l_{0/1}(y_i(w^Txi+b)-1)\tag{23}\label{eq23}$ 但是 $l_{0/1}$损失性质不好，因此常用 $l_{hinge}(z)$ 代替，因此$\eqref{eq23}$写为 $\min_{w,b}\quad \frac{1}{2}\|w\|^2+\lambda\sum_{i=1}^{n}\max(0, 1-y_i(w^Txi+b))\tag{24}\label{eq24}$ $\eqref{eq24}$所表示的优化目标(损失函数)由两部分组成，第一部分是结构风险(正则项)，第二部分是经验风险。因此常说SVM的损失函数是合页损失。

引入松弛变量 $\xi$ ，则$\eqref{eq24}$式写为 $\min_{w,b}\quad \frac{1}{2}\|w\|^2+\lambda\sum_{i=1}^{n}\xi_i\\ s.t.\quad y_i(w^Txi+b)\geq1-\xi_i\\ \xi_i\geq 0\tag{25}\label{eq25}$ 为什么是$\eqref{eq25}$式？

对于不满足约束的样本点，有 $\quad y_i(w^Txi+b)\leq 1\tag{26}\label{eq26}$ 因此对每个样本引入一个松弛变量 $\xi_i$，使得函数距离加上松弛变量大于1，即 $y_i(w^Txi+b)+\xi_i \geq 1\tag{27}\label{eq27}$ 针对$\eqref{eq25}$式的求解依然选择转化为求解对偶问题，这里不赘述。

第四部分：优缺点

==优点==

泛化性能好，不易过拟合
可在少数数据下获得较好结果
存在全局最优解
可处理非线性问题

==缺点==

大规模训练时速度慢
不适合多分类
对缺失数据，核函数敏感
- 没有处理缺失数据的机制
- 特征空间的好坏影响很大

第一部分：样本集线性可分

第二部分：样本集线性不可分

第三部分：软间隔与正则化

第四部分：优缺点

FEATURED TAGS