以下内容是翻译自papersapce上的Pytorch教程系列,目的是为了自己学习时候记录进度督促自己,另一方面也可供需要的人汲取。
pytorch 101 第一部分:理解图,自动微分和自动求导
提前准备:
-
链式法则
-
一点深度学习基础
-
PyTorch 1.0
可以在这里获得所有的代码。
自动微分
许多pytorch系列教程都会以初步讨论什么是基础结构为开始,然而在这里我们想先讨论一下自动微分。
自动微分是每个深度学习框架的基础,不仅仅是pytorch。我认为pytorch里面的自动微分机制,Autograd是一个理解自动微分如何工作的好工具,这会帮助我们更好理解pytorch及其他的深度学习库。
现在的神经网络结构动辄就有上百万的学习参数,从计算的角度来看,训练一个神经网络由两个部分组成:
- 前向传导来计算损失函数的值。
- 反向传播来计算参数的梯度。
前向传导就是直接从一层的输入传到输出。反向传播有一点复杂,因为需要使用链式法则根据损失函数来计算权重(参数)的梯度。
一个有趣的例子
让我们以一个只有5个神经元的神经网络为例。
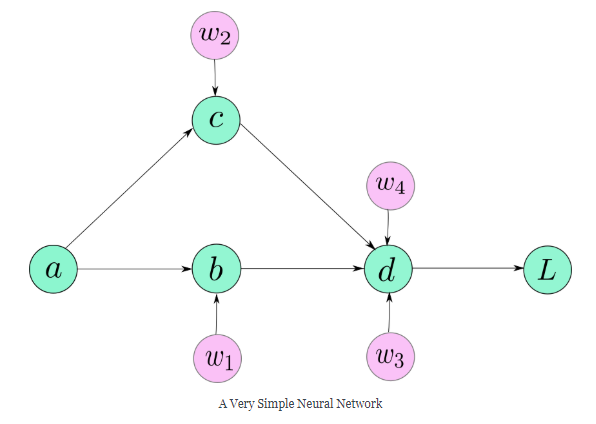
下式描述了我们的神经网络:
接下来为上面的每个参数w计算梯度。
这些梯度都可以通过链式法则计算出来,等式右侧的每个梯度都可以计算出来,因为每一项的分子都是分母的一个明确的函数。
计算图(Computation graph)
当网络比较简单的时候,我们可以手动计算梯度,但是想象一下,如果网络有152层呢?或者网络有多个分支。
当我们设计软件实现神经网络的时候,我们希望能有一个方法可以无缝地计算梯度而不用在乎网络结构,这样当网络发生改变就不用手动计算梯度。
计算图这种数据结构使得这一想法变成现实。计算图看起来就像是上图中所画的图表一样,不同的是计算图中的每个节点都是基础的操作,这些基础都是数学操作除了当我们需要表示一个用户定义的变量。
注意,为了清楚起见,我们已经在图中标记了叶子变量$\alpha, \omega_1, \omega_2, \omega_3, \omega_4$,但是它们都不是计算图的一部分,图中的$\alpha$是一个特例,因为它是用户自定义的变量。
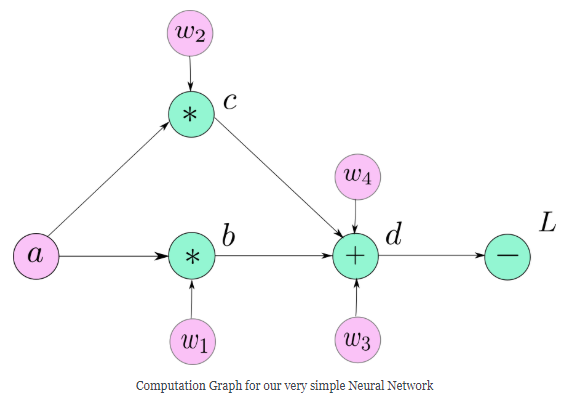
变量$b,c,d$都是数学计算的结果,而变量$\alpha, \omega_1, \omega_2, \omega_3, \omega_4$是由用户自己初始化,因为它们不是由任何数学运算创建的,所以与它们的创建相对应的节点由它们的名称本身表示,这个规则适用于图中的所有叶子节点。
计算梯度
现在我们准备讲一下如何使用计算图来计算梯度。
计算图中的每个节点和叶子节点可以认为是一个有输入和输出的函数,图中变量$d$是由$\omega_4 c和\omega_3 b$产生的,因此可以这样表示:
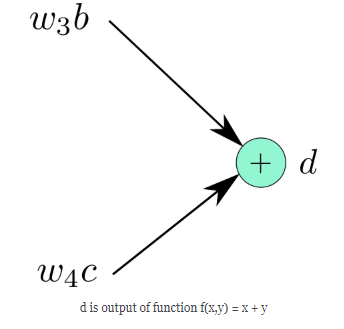
现在,我们就可以分别计算$f$对于输入的梯度$\frac{\partial f}{\partial \omega_3 b}$和$\frac{\partial f}{\partial \omega_4 c}$,然后分别以梯度标记进入节点的边,如下图所示。
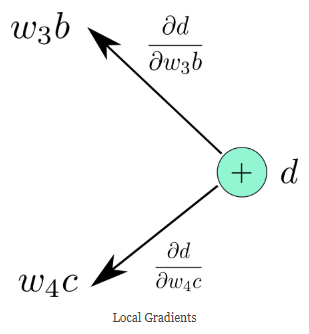
最后在整图上就是下面这样
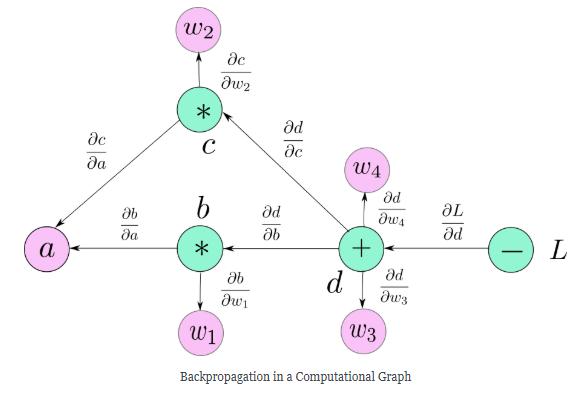
根据算法的描述,我们可以根据损失在图中计算任何一个节点的梯度,例如计算$\frac{\partial L}{\partial \omega_4}$:
- 首先找出所有可能的路径从$L$到$\omega_4$,只有一条这样的路径。
- 沿着这个路径乘所有的边。
如你所见,结果与用链式法则得到的一样。如果从$L$到一个变量的路径不止一条,我们就沿着每个路径乘以所有的边,最后把它们加起来。例如:
在神经网络中,我们能看到的只有网络的输入和输出,当有了输出,就可以计算loss,loss的大小反映了模型的学习能力,而模型的学习能力是由模型中大量的参数决定的,我们并不知道改变哪些参数可以使模型学习能变强,因此需要将loss从输出传递到输入,在反向传播的过程中就可以将所有的参数更新,也就是链式法则中从输出开始,到输入结束。
PyTorch Autograd
现在,我们知道了什么是计算图,让我们回到pytorch中理解如何实现。
Tensor
Tensor是pytorch中的一个基本的数据结构,类似于numpy中的array,还可以利用GPU的并行计算能力,Tensor语法类似于array。
Tensor这种数据结构可以快速的做线性代数运算,如果想在pytorch中创建这些操作的图,那么需要设置Tensor的requires_grad属性为True。
在pytorch中有许多Tensor初始化的方法,其中的一些方法可以很方便的设置requires_grad,而另一些则需要在创建Tensor后手动设置。

requires_grad具有“传染性”,意思是如果一个Tensor的创建是由其他Tensors得到的,并且至少有一个用于创建的Tensor的requires_grad为True,那么得到的Tensor的requires_grad将被设置为True。
每个Tensor都有一个称为grad_fn的属性,是一个创建变量的数学操作,如果requires_grad是False,那么grad_fn就是None。
在我们的例子中,$d=f(\omega_3 b, \omega_4 c)$,$d$的grad_fn是一个加操作,因为$f$把输入加了起来。注意,加操作同样也是一个节点,它输出$d$。如果Tensor是一个叶子节点(由用户初始化的),那么它的grad_fn同样也是None。
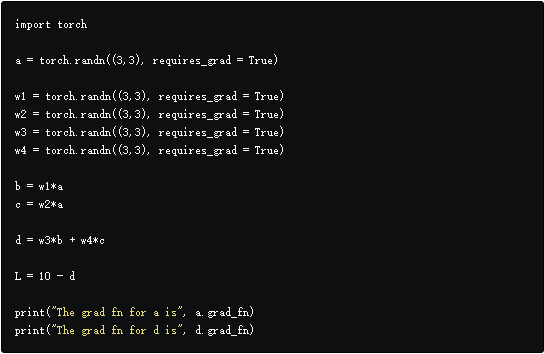
运行上面的代码就会得到下面的结果:

可以用is_leaf函数来判断一个Tensor是否是叶子节点。
Function
pytorch中的所有数学操作都在torch.nn.Autogrd.Function类中,这个类中有两个重要的函数需要特别留意。
第一个是forward函数,就是使用输入计算输出。
另一个就是backward函数利用前面网络传来的梯度。如你所见,从f反向传播的梯度基本上来自于它前面的的层反向传播到f的梯度乘以f的输出相对于输入的局部梯度,这正是反向传播的作用。
让我们再看一下例子
- d是一个Tensor,它的grad_fn是
,这是一个加操作,因为这个函数将d的两个输入加了起来。 - forward函数接收两个输入$\omega_3 b和\omega_4 c$并相加,然后把结果存在d中。
- backward函数把前面层的梯度做为输入。$\frac{\partial L}{\partial d}$是L到d的边,这个梯度存在d的grad属性中,可以通过d.grad获得。
- 接下来计算局部梯度$\frac{\partial d}{\partial \omega_4 c}$和$\frac{\partial d}{\partial \omega_3 b}$。
- backward函数将接收的梯度和局部梯度分别相乘并通过调用输入的grad_fn的backward方法将梯度作为输入。(这里写的比较绕,可以结合代码理解,就是递归一层层向前传播直到到达叶子节点)
- 例如,d的backward函数中调用了$\omega_4 c$的backward函数,当调用的时候,梯度$\frac{\partial L}{\partial d}*\frac{\partial d}{\partial \omega_4 c}$就被传递做为了输入。
- 现在,对于变量$\omega_4 c$,$\frac{\partial L}{\partial d}*\frac{\partial d}{\partial \omega_4 c}$做为输入的梯度,重复步骤3。
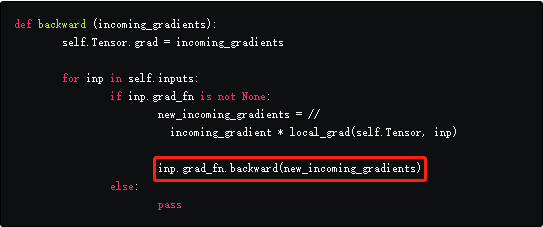
代码中,self.Tensor是Aurograd.Function创建的Tensor,就是例子中的d。
为了计算神经网络中的梯度,我们通常在loss中调用backward函数,然后从表示损失的grad_fn节点通过图回溯。当回溯的时候,backward函数被递归调用,一旦到达叶子节点,因为grad_fn是None,所以就停止在这条路径上回溯。需要注意的是,在pytorch中,如果在一个向量Tensor中调用backward的时候会报错,这表示只能在标量Tensor中调用backward。
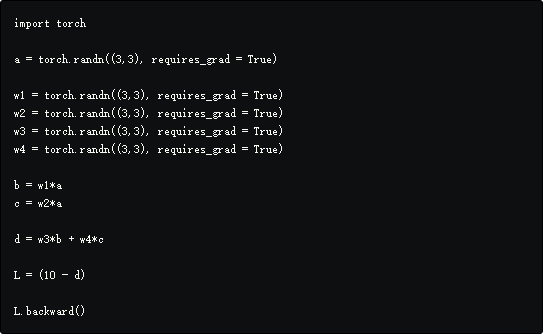
运行上面的代码会报错:

这是因为根据定义,梯度可以针对标量计算,但是无法求一个向量对另一个向量的导数,在数学中称为__Jacobian__,它的讨论已经超过了本章的范畴。
有两种方法来解决上面的问题:
- 如果在上面的代码上做一个小小的调整,使L成为所有损失的和,问题就会解决。可以通过调用Tensor的grad属性获得梯度。
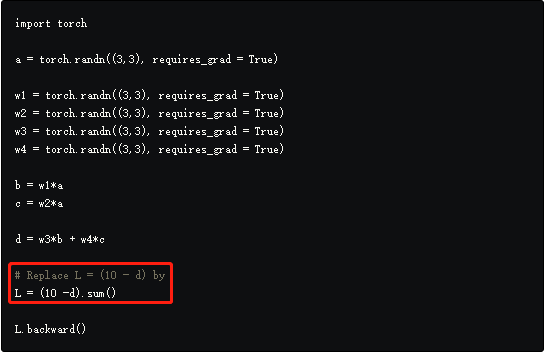
- 由于一些原因需要在一个向量函数上直接调用backward,可以传入一个torch.ones Tensor,size是需要调用backward的Tensor的size。

想一想backward如何将进来的梯度做为输入,通过上面的做法,backward认为进来的 梯度正好是一个size和L相同的Tensor,因此可以反向传播。用这种方法可以计算任何 Tensor的梯度,并且可以通过优化算法来更新。
PyTorch的计算图和TensorFlow的计算图有什么不同
PyTorch创建的图称为动态计算图,意思就是图是动态生成的,除非调用forward函数,否则图中没有任何Tensor节点。
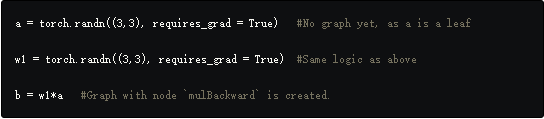
图在Tensor调用了forward函数后创建,随后为图和中间值分配非叶子节点的缓冲区。当调用backward时,随着梯度的计算,这些缓冲区实际上被释放,计算图销毁(从某种意义上讲,由于缓冲区保存的值已经消失,所以无法反向传播)。下一次会在同样的Tensors集合上调用forward,之前的叶子节点缓冲区会共享,非叶子节点缓冲区会重新创建。
如果在一个非叶子节点上不止一次调用backward,那么就会遇到下面的错误:
1
RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.
这是因为在第一次调用backward时非叶子节点缓冲区就被销毁,因此再次调用时没有路径引导到叶子节点。可以通过在backward函数中加入retaing_graph=True来避免非叶子节点缓冲区的释放。

这样就可以在同一张计算图上再次反向传播,并且梯度也会积累,既下一次反向传播时,梯度将会加在之前的结果上。
这与TensorFlow中的静态计算图,在运行程序之前定义图,不同,通过给预先定义的图喂数据来”run”。
动态图允许在运行期间更改网络结构,因为图是在backward调用后才创建。这意味着可以在程序的生命周期内重新定义图形,因为不必事先定义它,但是在静态图中就不可以。
动态图使得Debug更加简单,因为可以很容易的定位到错误的源头。
一些技巧
requires_grad
这是Tensor类的属性,默认为False,当需要冻结一些层的时候提供便利,并且可以在训练的时候阻止参数更新。当设置requires_grad为False的时候,这些Tensor就不参与计算图。
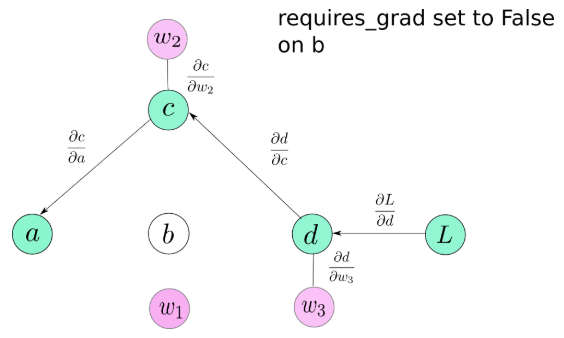
因此,没有梯度会传递到它们,也不会传播到那些依赖于这些层以获得梯度流的层,当设置requires_grad为True,由于传染性,即使在运算中只有一个操作数的requires_grad为True,结果也是True。
torch.no_grad()
当我们在计算梯度时,需要高速缓存输入数据和中间结果,因为在稍后的梯度计算中可能需要。例如在计算$b=\omega_1 *\alpha$,$\alpha$和$\omega_1$分别是输入,我们需要保存这些值以便反向传播使用,这会影响网络的内存分配。
当在做推断的时候,我们不需要计算梯度,因此不需要保存这些结果,事实上推断的时候不需要创建图,因为这会白白浪费内存,因此,PyTorch提供了一个上下文管理器torch.no_grad,在这个管理器下不会创建图。

总结
理解Autograd和计算图的工作原理可以使得用PyTorch工作更加简单,在我们坚实的基础下,下一节将会详细介绍如何创建自定义复杂体系结构,如何创建自定义数据管道和更有趣的东西。